WARNING - This is a very long article and goes into great detail about how we have been approximating, and how we plan plan to approximate muzzle velocities for the handguns in our database. We wanted to provide as much information as possible for anyone who had questions about our rationale and methods for approximating muzzle velocities. But, unless you are a physics/mathematics/spreadsheet wonk you may not want to make it all the way through this article and associated documentation.
First, before going any further we want to offer a shout-out and sincere thanks to the folks at BallisticsByTheInch.com (BBTI). Their real-world tests of muzzle velocities in relation to barrel lengths, and their tests on the impact of revolver cylinder-gap on muzzle velocity were instrumental in validating the accuracy of our approximation formulas.
That being said, here is a summary of the discussion points in this article for those of you who are just interested in the bottom line: In Part 1 we discuss the difference in the way pistol barrels and revolver barrels are measured and how that affects the accuracy of our approximations for certain handguns. Part 2 is a short discussion about where we get real ballistics data to use in our approximation formulas. In Part 3 we discuss and explain the current approximation formula that we developed in-house and have been using for some time. We also reveal the formula's fundamental flaws and inaccuracies that we plan to address in this project. Our search for a more accurate formula is laid out in Part 4. In Part 5 we go over the logic and formulas we plan to implement to get "true" barrel lengths for our muzzle velocity calculations. Parts 6 and 7 discuss in detail and explain the muzzle velocity formulas that we discovered in our search, and subsequently tested. Finally, in Part 8 we discuss our formula verification process using the real test data from the folks at BBTI, and the formula selection we made based on the results.
Introduction:
In our article "Selecting a Representative Cartridge" we discussed the process for selecting a set of representative cartridge specifications for the 55 calibers used in our database. Now we will look at how we approximate the cartridge's muzzle velocity (and subsequently muzzle energy and other rankings) by adjusting for the difference between the industry standard test barrel used for obtaining a cartridge's ballistics specifications and the actual handgun barrel from which the cartridge will be fired.
Part 1: Pistol Barrels versus Revolver Barrels
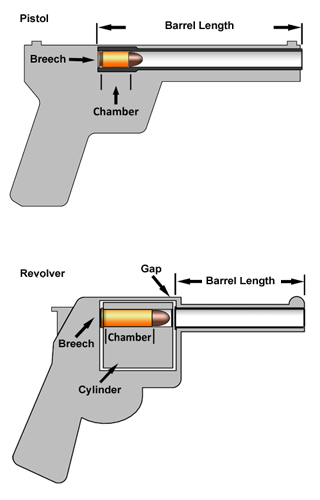
The first thing to note is that there is a fundamental difference in the way pistol and revolver barrel lengths are measured. When measuring a pistol's barrel length the barrel's cartridge chamber is included in that measurement. This is due to the fact that a pistol's barrel and cartridge chamber are integrated together into a solid one-piece barrel assembly. A pistol barrel that measures 5 inches in length includes the 1 to 2 inches of cartridge chamber length, so the true bullet travel through a pistol's 5 inch barrel is closer to 3 to 4 inches.
Conversely, a revolver's barrel is measured from its muzzle to the front of the revolver's cylinder. This is because a revolver barrel is separate form the cartridge chamber. So, the true bullet travel through a revolver's 4 inch barrel is actually 4 inches. Additionally, when it comes to measuring muzzle velocity a revolver introduces a gap between the cylinder and barrel. Escaping gasses through this gap when a revolver is fired can reduce a bullet's muzzle velocity. When true revolver cartridges are measured for muzzle velocity they are done so with test barrels that include a gap to more accurately represent the revolver. These are called "vented" test barrels.
Now to complicate things a bit, some revolvers are made to fire pistol or rifle cartridges and some pistols are made to fire revolver cartridges. We call these cartridges "cross-over" cartridges. So, when those cartridges for which the industry specification tests are performed using rifle or pistol barrels are instead used in a revolver, the calculated adjusted muzzle velocity must include an approximated compensation for the revolver's cylinder gap. This is the same for calibers who's industry specification tests are done with "vented" barrels that are subsequently used in a pistol. In those cases the test specifications need to have an increased compensation approximated to make up for the gap introduced in the test data. How we intended to do this approximation explained in a separate article titled "Cylinder Gap Compensation".
Part 2: Industry Standard Measurements
When it comes to approximating muzzle velocities for various barrel lengths we have to start with some real data. As stated in our article on cartridge selection we use industry standard test data. Ballistic specifications for a particular cartridge of a given caliber are based on actual measurements from tests performed by both SAAMI and the ammo manufacturers. These tests are typically done using special ballistic test barrels, again based on SAAMI specifications. So, a given empirical muzzle velocity and muzzle energy measured for a cartridge and provided by the manufacturer is only accurate for the specific length and type of barrel in which it was tested.

When it comes to determining what a cartridge's ballistics will be for an actual firearm, again the only truly accurate method would be to take real-world empirical measurements with the gun. Unfortunately, this is not an option for the over 5,000 handgun variants that we currently have in our database. The next best thing is to make approximations based on the available test data. The key parameter that must be derived is Muzzle Velocity. Other derived parameters such as Muzzle Energy, Recoil Factor and Defense Factor all rely on an accurate approximation of the gun's Muzzle Velocity.
Part 3: How We've Been Doing It
When we began developing this website ten years ago we knew we would have to somehow approximate muzzle velocity for different barrel lengths. We started with an old shooter's adage; "On average you loose about 25 ft/sec for every inch of barrel length shortened." Then we made an assumption that the "average" bullet weight for that adage was 200 grains.
Given those two values (200 grain bullet, 25 ft/sec/in) we developed a simple formula that we have been using ever since. In our formula we take the log of the ratio between the the "average" bullet weight (200 gr) and the test bullet weight, and multiply it with the "average" muzzle velocity per inch (25 ft/sec). Then we multiply that value by the difference between the reference and selected barrel lengths, and add (or subtract) that offset to the test cartridge muzzle velocity to get an adjusted muzzle velocity.

While this approximation formula has served us relatively well, over the years we have become aware of several fundamental flaws and inaccuracies in its calculations. First and foremost is that the formula does not take into account the different ways that pistol and revolver barrels are measured. While this is not as much of an issue when comparing similar types of handguns, it is not so accurate when comparing pistols to revolvers. Accuracy is also lost on "cross-over" handguns; pistols chambered for revolver cartridges and revolvers chambered for pistol or rifle cartridges. Finally, the formula does not take into account any of the handgun's "internal ballistics" which affects the accuracy of the calculations the further from the average (200 grains) a given caliber weight may be, or the greater the difference is between the caliber's test reference barrel length and the actual handgun barrel length.
Part 4: Search for a Better Formula
Desiring to be as accurate and truthful as possible with our rankings, last year we began a quest to find a formula (or formulas) that took into account all of the relevant factors mentioned above. Not long into that research we discovered Homer S. Powley.
Now, there are many notable names in firearms and shooting history; John Browning, Samuel Colt, Jeff Cooper, Jack Weaver, Ray Chapman, Julian Hatcher, John Taylor, just to name a few from our list. But, Homer Powley's name most likely won't make anyone's list. Although, it should. Powley was a chemist, mathematician and author who performed pioneering work in exterior and interior firearm ballistics in the 1960's. He was the inventor of the Powley Computer and the Speer Ballistics Calculators. These were slide-rule-like calculators of the time used for determining a number of different ballistics parameters. His internal ballistics equations are the basis for many of the software and online cartridge loading calculators around today.
What we seized upon from Powley is a series of formulas he developed for approximating muzzle velocity based on barrel length using actual cartridge test data as the seed -exactly what we were looking for. The premise behind the formulas is the Expansion Ratio, which is the number of times the gas of a fired cartridge will expand by the time the bullet reaches the muzzle. Here are a couple of quotes from Powley:
"First contemplation of the problems of Interior Ballistics gives the impression that they should yield rather easily to relatively simple methods of analysis. Further study shows the subject to be of almost unbelievable complexity."
"A gun with low Expansion Ratio and a high ratio of Powder Charge to Bullet Weight will be affected much more by barrel shortening than will a gun of both high Expansion Ratio and low ratio of Powder Charge to Bullet Weight."
Finding references to Powley's formulas was not easy. Fifty-year-old works by an otherwise unknown mathematician are hard to come by. We were able to find three (unverified) variants of Powley's formulas through a bunch of online research. Two of the variants (we call Powley1 and Powley2) actually use the same formulas, but with different constant values. They are complex formulas that take into account the bullet weight and length as well as gunpowder charge weight, along with barrel dimensions. The third (Powley3) is a condensed version of Powley's original formulas that relies solely on expansion ratios derived simply from chamber and bore volumes.
Part 5: Barrel Length Logic and Formulas
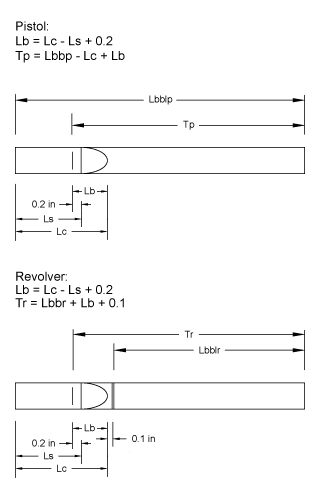
Before we can use any the muzzle velocity formulas we first have to get an accurate value for the barrel lengths through which the bullet actually travels. This is done with calculations that are based on the handgun type (pistol or revolver) and the cartridge dimensions. Refer to the the pistol and revolver barrel diagrams above.

The result value "T" in the formula becomes the working barrel length for determining bore volumes that will be used in the subsequent formulas.
Part 6: The First Powley Formulas (Powley1 and Powley2)
We discovered this first formula attributed to Powley in a firearms forum post from 2010. It uses the cartridge's bullet weight and gunpowder charge weight in its calculation to determine the test barrel Expansion Ratio. It then factors that Expansion Ratio along with the ratio of the original test bore volume and the new barrel bore volume to determine the Expansion Ratio of the new barrel. It finally calculates the new barrel muzzle velocity based again on the cartridge's bullet weight and gunpowder charge weight, along with the new calculated Expansion Ratio. We were actually able to verify this formula reference from an old NRA publication "Handloading" book and article "Some Simplified Interior Ballistics for Handloaders" by WM. C. DAVIS, JR.. What we could not find anywhere was a reference for the constant "8000" used in this equation. We did find another forum post from 2014 though, where the writer discusses using "8958" instead of "8000" in Powley's equation. The source of this second constant stated that Powley never indicated how he determined the constant 8000, but stated that he himself adjusted the value to 8958 as a correction factor to allow for friction, rotational inertia, heat loss, and air compression in the barrel ahead of the projectile. This warranted an analysis of both constants. So, in our verification tests we decided to test both. In our analysis, formula "Powley1" uses 8000 and formula "Powley2" uses 8958.


Part 7: The Second Powley Formula
While we were able to find two independent resources for the first Powley formula above, we still had unanswered questions about the constant(s) used in the equations. So, we continued our online search for more resources, formulas and references related to Powley's internal ballistics research. This led us to a post by Bill Moyer back in 2017 on the metaCPAN website. The Comprehensive Perl Archive Network (CPAN) is an open-source software repository of over 250,000 programming software modules and accompanying documentation for programs written in the Perl programming language by over 12,000 contributors. Mr. Moyer graciously provided a series of Perl routines for various internal ballistics calculations, including one listed as "Powley" which he states "implements Powley's formula for approximating the projectile velocity gained or lost from a change in barrel length." We reverse-engineered his "Powley" Perl routine and developed the subsequent formula.

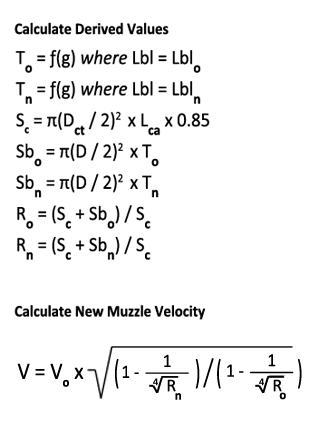
This version of Powley's original formula simply relies on expansion ratios that are derived solely from chamber and bore volumes. It does not use bullet or gunpowder charge weights, and does not include any referenced constants to reconcile. The only constant in this equation is 0.85 which is used in calculating the "chamber volume" Sc. The assumption is that you take the total chamber volume calculated by a cartridge's case length and diameter, and reduce it to 85% to make up for the thickness of the case's primer base and the space occupied by the seated bullet.
Part 8: Verification of Formulas
Now that we have a number of formulas for approximating muzzle velocity we need a way to verify each of the formulas for accuracy. What we need in order to do this are some true empirical measurements against which we can compare the formulas' results.
This is where the folks at BBTI come in. In order to answer the age-old question of muzzle velocity versus barrel length BBTI took on the herculean task of actually taking inch-by-inch muzzle velocity measurements for nearly 150 different cartridge loads across 23 different calibers. This was a costly and time consuming endeavor; thousands of rounds fired, many custom test barrels progressively chopped and crowned inch-by-inch, the meticulous recording of each chronograph measurement. We sincerely thank them for making this data available.
Our verification process began with collecting and averaging BBTI test data for a select number of calibers across their range of test barrel lengths. We then took our four formulas and converted them into computer routines written in our website's native programming language, and then ran these routines against the same selected calibers and barrel lengths comparing the results side-by-side with the BBTI test data. Now, BBTI tested a number of rifle, pistol and revolver cartridges. But, in all of their tests they used solid test barrels with no "vent" or gap, and all barrel lengths were measured from muzzle to breech face regardless of cartridge type. Because of this we could not get a direct match between industry standard tests of revolver cartridges using "vented" barrels and BBTI's tests of the same cartridges through solid barrels. As such, we decided to stick with just pistol and rifle cartridges that BBTI tested for our verification tests. Those cartridge calibers are .22 LR, .25 Auto, .380 Auto, 9 mm, 357 SIG, .40 S&W, .45 Auto and .223 Remington.
Here's an example of the verification results for the 9 mm cartridge:

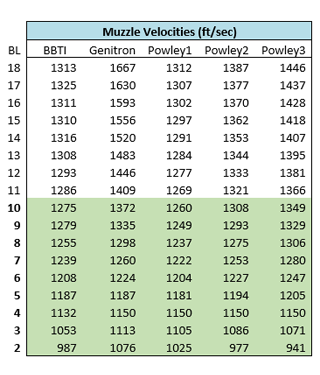
While in this example the "Powley2" equation has the best accuracy for the 9 mm caliber, ultimately we selected the "Powley3" equation, as it had the best overall accuracy and the least maximum velocity difference averaged across all calibers in the verification tests.
The following tables summarize the verification results across the eight selected calibers:
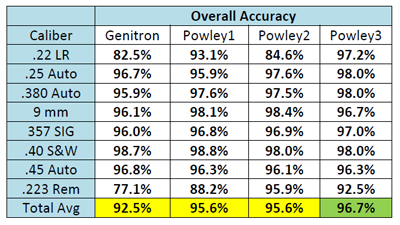
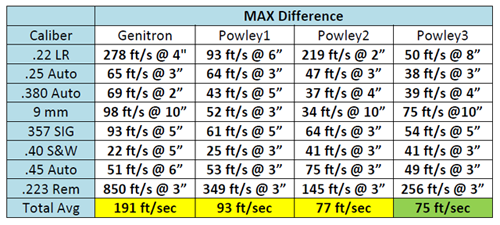
For an even deeper dive into the details and numbers from these tests refer to this PDF document: Muzzle Velocity Formula Verification.